Wheeled Robot Motion
In this post we will analyze the motion of a simple 2-wheeled robot, shown in the image below. The analysis will result
in wheel velocity command equations for reaching a target.
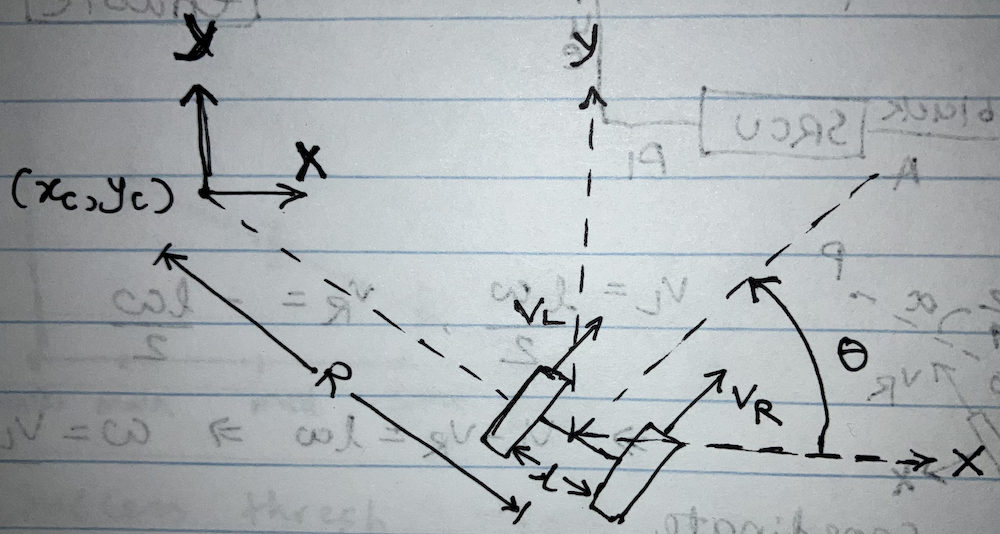
Notation
- The robot operates in the XY plane and has a gap $l$ between its wheels, which move with linear velocities $v_L$ and $v_R$.
- Its current position is $(x, y)$ and heading is $\theta$.
- The resultant of the two wheels’ motion will result in a circular trajectory about an “instantaneous center of rotation” (ICC) $(x_c, y_c)$, which keeps changing every instant as the wheel velocities change.
- The ICC is at a distance $R$ from the robot center. Note that $R = 0$ and $R = \inf$ are possible when $v_L = -v_R$ and $v_L = v_R$ respectively.
Forward Dynamics
This means the effect in task space (XY plane) of a given set of wheel velocities. Denoting the rotational velocity about the ICC as $\omega$, we have
\[\begin{align} v_L &= \left( R - \frac{l}{2} \right) \omega \\ v_R &= \left( R + \frac{l}{2} \right) \omega \end{align}\]Solving for $\omega$ and $R$ gives
\[\begin{equation} \omega = \frac{v_R - v_L}{l} \end{equation}\]and
\[\begin{align} R &= \frac{v_R + v_L}{2 \omega}\\ &= \frac{l}{2} \left( \frac{v_R + v_L}{v_R - v_L} \right) \end{align}\]Thus, the robot moves in the XY plane about the ICC at distance $R$ from the robot center, with an angular velocity $\omega$. The actual ICC location is given by
\[\begin{equation*} (x_c, y_c) = (x - R \sin(\theta), y + R \cos(\theta)) \end{equation*}\]Writing the equation for the new position of the robot after motion for $\Delta t$ time in matrix form,
\[\begin{bmatrix}x' \\ y' \\ \theta' \end{bmatrix} = \begin{bmatrix} \cos(\omega \Delta t) & -\sin(\omega \Delta t) & 0\\ \sin(\omega \Delta t) & \cos(\omega \Delta t) & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}x - x_c \\ y - y_c \\ \theta \end{bmatrix} + \begin{bmatrix}x_c \\ y_c \\ \omega \Delta t \end{bmatrix}\]where we first translate to the ICC coordinate system, rotate, and then translate back to the world coordinate system.
Inverse Dynamics
Given a target robot location $(x’, y’)$, what wheel velocities $v_L$, $v_R$ should we apply? Note from (1) and (2) that we need $R$ and $\omega$ for that calculation. Writing out the matrix equation above, and substituting $x - x_c = R \sin (\theta)$, $y - y_c = -R \cos (\theta)$,
\[\begin{align} x' &= \cos(\omega \Delta t) R \sin (\theta) + \sin(\omega \Delta t) R \cos(\theta) + x - R \sin(\theta)\\ x' - x = \Delta x &= (\cos(\omega \Delta t) - 1) R \sin (\theta) + \sin(\omega \Delta t) R \cos(\theta) \end{align}\]and
\[\begin{align} y' &= \sin(\omega \Delta t) R \sin (\theta) - \cos(\omega \Delta t) R \cos(\theta) + y + R \cos(\theta)\\ y' - y = \Delta y &= \sin(\omega \Delta t) R \sin (\theta) + (1 - \cos(\omega \Delta t)) R \cos (\theta) \end{align}\]From (7) and (9) we get
\[\begin{align} \Delta y \sin(\theta) + \Delta x \cos (\theta) &= R \sin(\omega \Delta t),\\ \Delta y \cos(\theta) - \Delta x \sin (\theta) &= R (1 - \cos(\omega \Delta t)) \end{align}\]Dividing (10) by (11) we get
\[\begin{align} \frac{1 - \cos(\omega \Delta t)}{\sin(\omega \Delta t)} &= \frac{\Delta y \cos(\theta) - \Delta x \sin (\theta)}{\Delta y \sin(\theta) + \Delta x \cos (\theta)}\\ \implies \frac{2 \sin^2 (\frac{\omega \Delta t}{2})}{2 \sin (\frac{\omega \Delta t}{2}) cos (\frac{\omega \Delta t}{2})} &= \frac{\Delta y \cos(\theta) - \Delta x \sin (\theta)}{\Delta y \sin(\theta) + \Delta x \cos (\theta)}\\ \implies \tan(\frac{\omega \Delta t}{2}) &= \frac{\Delta y \cos(\theta) - \Delta x \sin (\theta)}{\Delta y \sin(\theta) + \Delta x \cos (\theta)}\\ \implies \omega &= \frac{2}{\Delta t} \frac{\Delta y \cos(\theta) - \Delta x \sin (\theta)}{\Delta y \sin(\theta) + \Delta x \cos (\theta)} \end{align}\](10)$^2$ + (11)$^2$ gives
\[\begin{align} (\Delta y \sin(\theta) + \Delta x \cos (\theta))^2 + (\Delta y \cos(\theta) - \Delta x \sin (\theta))^2 &= R^2 \sin^2(\omega \Delta t) + R^2 (1 - \cos(\omega \Delta t))^2\\ \implies \Delta x^2 + \Delta y^2 &= 2 R^2 (1 - \cos(\omega \Delta t)) \end{align}\]Substituting $1 - \cos(\omega \Delta t) = \frac{\Delta y \cos(\theta) - \Delta x \sin (\theta)}{R}$ from (11), we get
\[\begin{align} \Delta x^2 + \Delta y^2 &= 2R (\Delta y \cos(\theta) - \Delta x \sin (\theta))\\ \implies R &= \frac{\Delta x^2 + \Delta y^2}{2 (\Delta y \cos(\theta) - \Delta x \sin (\theta))} \end{align}\]Finally, we can calculate $v_L$ and $v_R$ by substituting the values of $R$ and $\omega$ from (19) and (15) into (1) and (2). This is left as an exercise to the reader.